命題22
もし、任意個の奇数が一緒に加えられ、それらの個数が偶数ならば、その総和は偶数である。

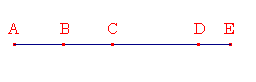
任意個の奇数AB、BC、CD、DEが個数は偶数で、一緒に加えられたとせよ。
その総和AEは偶数であると主張する。
AB、BC、CD、DEのそれぞれは奇数なので、もし、それぞれから単位が引かれれば、残りのそれぞれは偶数で、つまり、それらの総和は偶数である。
しかし、単位の個数もまた偶数である。
それゆえに、その総和AEもまた偶数である。propositionⅨ21
それゆえに、もし、任意個の奇数が一緒に加えられ、それらの個数が偶数ならば、その総和は偶数である。